Conditionals 1

Introduction

This chapter introduces the main concepts related to Boolean logic. In particular, we refer to Boolean values (i.e., True and False), and how they can be used in Boolean expressions to support conditional executions within a program.

Logic

Logic is the study of the formal principles of reasoning. These principles determine what can be considered as a correct or incorrect argument. An argument is “a change of reasoning that ends up in a conclusion” (Beecher, 2017). Every statement within an argument is called a proposition, and it has a truth value. That is, it is either true or false. Thus, certain expressions like questions (e.g. “are you hungry?”) or commands (e.g. “clean your bedroom!”) cannot be propositions given that they do not have a truth value.

Below we present a very famous argument in the logic field:

1. Socrates is a man.

2. All men are mortal.

3. Therefore, Socrates is mortal.

This argument is composed of three propositions (each one is enumerated). These statements are propositions because all of them have a truth value. However, you can notice that some of these statements are used to arrive at a conclusion. The propositions that form the basis of an argument are known as premises. In our example, propositions 1 and 2 are premises. Lastly, the proposition that is derived from a set of premises is known as a conclusion.

EXTRA

Logic studies the formal principles of reasoning, which determine if an argument is correct or not. An argument is a sequence of premises. Each premise is a statement that has a truth value (i.e. true or false).

Types of Arguments

Arguments can either be deductive or inductive.

Deductive Arguments

Deductive arguments are considered a strong form of reasoning because the conclusion is derived from previous premises. However, deductive arguments can fail in two different scenarios:

False premises: One of the premises turns to be false. For example:

1. I eat healthy food.

2. Every person eating healthy food is tall.

3. I am tall.

In this example, premise 2 is false. It is not true that every person eating healthy food is tall. Then, this argument fails.

Faulty logic: The conclusion is wrongly derived out from the premises. For example:

1. All bitterballen are round.

2. The moon is round.

3. The moon is a bitterbal.

In this case, the conclusion presented in premise 3 is false. It is true that bitterballen are round and that the moon is round, but this does not imply that the moon is a bitterbal! By the way, a “bitterbal” is a typical Dutch snack, to be eaten with a good glass of beer!

Inductive Arguments

Although deductive arguments are strong, they follow very stern standards that make them difficult to build. Additionally, the real world usually cannot be seen just in black and white–there are many shades in between. This is where inductive arguments play an important role. Inductive arguments do not have an unquestionable truth value. Instead, they deal with probabilities to express the level of confidence in them. Thus, the conclusion of the argument cannot be guaranteed to be true, but you can have a certain confidence in it. An example of an inductive argument comes as follows:

1. Every time I go out home it is raining.

2. Tomorrow I will go out from home.

3. Tomorrow it will be raining.

There is no way you can be certain that tomorrow will rain, but given the evidence, there is a high chance that it will be the case. (The chance might be even higher if we mention that we are living in the Netherlands!)

EXTRA

Arguments can be either deductive or inductive. On the one hand, deductive arguments have premises that have a clear truth value. On the other hand, inductive arguments have premises associated with a level of confidence in them.

4. Boolean Logic

Given their binary nature, computers are well suited to deal with deductive reasoning (rather than inductive). To allow them to reason about the correctness of an argument, we use Boolean logic. Boolean logic is a form of logic that deals with deductive arguments–that is, arguments having propositions with a truth value that is either true or false. Boolean logic or Boolean algebra was introduced by George Boole (that is why it is called Boolean) in his book “The Mathematical Analysis of Logic” in 1847. It deals with binary variables (with true or false values) representing propositions and logical operations on them.

Logical Operators

The main logical operators used in Boolean logic to connect propositions are:

1. And operator: It is also known as the conjunction operator. It chains premises in such a way that all of them must be true for the conclusion to be true.

2. Or operator: It is also known as the disjunction operator. It connects premises in such a way that at least one of them must be true for the conclusion to be true.

3. Not operator: It is also known as the negation operator. It modifies the value of a proposition by flipping its truth value.

Venn diagrams of the and, or, and not logical operators.

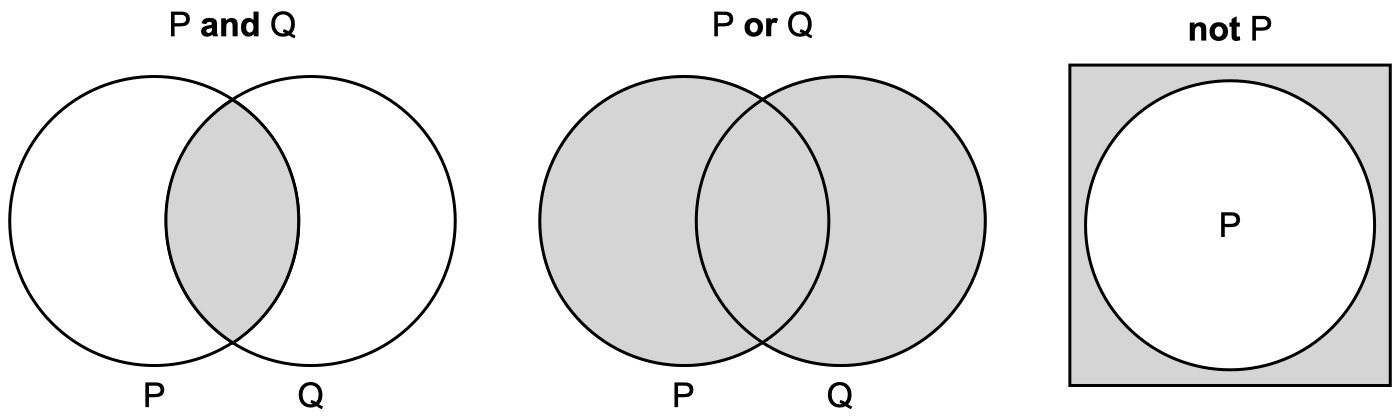
In Boolean logic, propositions are usually represented as letters or variables (see previous figure). For instance, going back to our Socrates argument, we can represent the three propositions as follows:

• P: Socrates is a man.

• Q: All men are mortal.

• R: Therefore, Socrates is mortal.

In order for R to be true, P and Q most be true.

Boolean Expressions

Let us now see how Boolean logic is supported in Python!

A boolean expression is an expression that yields either True or False.

The following examples use the operator == to compare the values of two expressions. The result is True if the values are the same, otherwise the result is False.

5 == 5

True

5 == 6

False

True and False are special values of the type bool.

True and False

False

Besides the relational operator == we have

Operator	Purpose
==	x is equal to y
!=	x is not equal to y
x > y	x is greater than y
x < y	x is less than y
x >= y	x is greater than or equal to y

Although these operations are probably familiar to you, the Python symbols are different from the mathematical symbols.

A common error is to use a single equal sign (=) instead of a double equal sign (==).

Remember that = is an assignment operator and == is a relational operator.

Logical Operators

There are the three Python logical operators: and, or, and not. The semantics (meaning) of these operators is the same one as the one presented in the Boolean Logic section.

Operator	Technical name	Math symbol	Python construct
And	Conjunction	\(\land\)	and
Or	Disjunction	\(\lor\)	or
Not	Negation	\(\lnot\)	not

They can be used in combination with Boolean expressions, as follows.

x: int = 9
x > 0 and x < 10

True

n % 2 == 0 or n % 3 == 0 is True if either one or both of the conditions are True—that is, if the number is divisible by 2 or 3.

n: int = 27
n % 2 == 0 or n % 3 == 0

True

Finally, the not operator negates a boolean expression, so not (x > y) is True if x > y is False, that is, if x is less than or equal to y.

x: int = 10
y: int = 15
not (x > y)

True

Strictly speaking, the operands of the logical operators should be Boolean expressions, but Python is not very strict. Any non-zero number is interpreted as True. This flexibility can be useful, but there are some subtleties to it that might be confusing. You might want to avoid it (unless you know what you are doing).

If you use the Boolean operators in the same expression you have to beware of their precedence order. The order is as follows: not > or > and, again if in doubt use brackets!

not False and True

True

True or False and True

True

Conditional Execution

In order to write useful programs, under certain situations, we need to check if a set of conditions are fulfilled and change the behavior of the program accordingly. Conditions allow us to change the execution flow in a program.

Conditional statements provide us with this functionality. The simplest form of a conditional statement is the if statement.

x: int = 10
if x > 0:
    print('x is positive')
    
print('x is an integer value')

x is positive
x is an integer value

The Boolean expression after the if keyword is called the condition. If it is true, then the indented statement is being executed.

If statements have a header (aka. condition) followed by an indented body. Statements like this are called compound statements.

What is printed when executing the following cells?

x: int = 1
if x < 0:
    print('x is negative')
    
print('Hello Data Scientists')

Hello Data Scientists

x: int = 1
if x < 0:
print('x is negative')

print('Hello Data Scientists')

  Cell In[11], line 3
    print('x is negative')
    ^
IndentationError: expected an indented block

Where other programming languages use brackets, for instance { and } in C or Java, Python uses indentation to group lists of instruction blocks.

x: int = -1
if x < 0:
    print('x is negative')
    print('Hello Data Scientists')

Do It Yourself!

Ask the age of a user with the input function. If the user is an adult (older than or equal to 18) print the message “Hi adult!”.

# Remove this line and add your code here

Sometimes conditionals are not really needed; using a Boolean expression is sufficient. Having unneeded language constructs (e.g. conditionals) can negatively impact the readability of your code.

Let us see an example.

# Change the truth values of p and q to see how the conclusion r changes
p: bool = True
q: bool = True
r: bool

if p and q:
    r = True
else:
    r = False
    
print(r)

The previous translation to Python code of the deductive argument is correct, however, we can get rid of the conditional statement! Let us see.

# Change the truth values of p and q to see how the conclusion r changes
p: bool = True
q: bool = True
r: bool = p and q
    
print(r)

Alternative Execution

There is yet another if statement to represent an alternative execution. This statement is calles an if-else statement. There are 2 alternatives to execute and the evaluation of the expression determines which alternative needs to be executed. If the condition is true the body of the if section will be executed. However, if the condition is false, the body of the else section will be executed.

x: int = 23

if  x % 2 == 0:
    print('x is even')
else:
    print('x is odd')

Do It Yourself!

Ask the age of a user with the input function. If the user is an adult (older than or equal to 18) print the message “Hi adult!”, otherwise print the message “Hi kid!”.

# Remove this line and add your code here

Chained Conditionals

Sometimes there are more than 2 alternatives. In that case you can use a chained conditional. A chained contidional starts with the well-known if section, it ends with the else one, and all othar alternative executions placed in the middle, are preceeded by an elif section. elif is an abbreviation of else if. After the elif keyword you should always define a new Boolean expression.

x: int = 4
y: int = 2

if  x < y:
    print('x is less than y')
elif x > y:
    print('x is greater than y')
else:
    print('x and y are equal')

Conditions in a chained condition are checked from top to bottom, and as soon as one succeeds the corresponding branch is executed and the conditional terminates.

If more than one condition evaluates to True only the first branch for which the condition succeeds is executed.

Do It Yourself!

Ask the age of a user with the input function. If the user is a kid (younger than 18) print the message “Hi kid!”; if the user is between 18 and 69 print the message “Hi adult!”; otherwise, print the message “Hi old pal!”.

# Remove this line and add your code here

Nested Conditionals

One conditional can also be nested within another. That is, you can have a contidional statement within the body of one of the alternative executions of a conditional.

x: int = 2
y: int = 2

if x == y:
    print('x and y are equal')
else:
    if x < y:
        print('x is less than y')
    else:
        print('x is greater than y')

In the prvious example, the outer conditional contains two branches. The first branch contains a simple statement that prints the message “x and y are equal”. The second branch contains another if statement, which has two branches of its own.

EXTRA

Although the indentation of the statements makes the structure apparent, nested conditionals become difficult to read very quickly. It is a good idea to avoid them whenever you can. Logical operators often provide a way to simplify nested conditional statements.

x: int = 2

if 0 < x:
    if x < 10:
        print('x is a positive single-digit number')

We can refactor this nested conditional by introducing the and operator in the logical expression.

x: int = 2

if  0 < x and x < 10:
    print('x is a positive single-digit number')

We can refactor this nested conditional by merging the two conditions into 0 < x < 10.

x: int = 3

if 0 < x < 10:
    print('x is a positive single-digit number')

Do It Yourself!

Can you refactor the following program so we avoid having nested conditionals?

# Modify this code
day = 2

if day < 3:
    print('The week just started')
else:
    if day <= 5:
        print('We are just in the middle of the week')
    else:
        if day < 7:
            print('The week is ending')
        else:
            print('It is a fact, the week ends today')

Catching Exceptions

The following program requests you to enter your age. Then, it parses the input as an integer. But what does happen if you introduce a string that cannot be converted into a number?

age: str = input('What is your age? ')
int(age)

Indeed, you get an error or exception.

Python can help you handle these cases to end the program gracefully, or continue through an alternative path. The construct that handles errors is called try-except.

We use the try-except statement when we know that a sequence of instructions might introduce an error (placed in the try section) and you want to execute other sequence in case the problem rises (placed in the except section). If no error appears, the except section is ignored. Catching is the action of handling an exception.

Now, let us rewrite our previous example with the try/except construct.

age: str = input('What is your age? ')

try:
    # The int(age) call can rise an exception
    print(int(age))
except:
    print('You should introduce a number!')

Do It Yourself!

Ask the user for two numbers (two calls of the input function can be used) so you can compute the addition of both of them. Then, print the message “num_1 + num_2 = sum”. If the user inputs a value that cannot be converted to a number print the message “Please, enter a valid number.”

# Remove this line and add your code here

Short-circuit Evaluation of Logical Expressions

When Python processes a logical expression, it does it from left to right.

So, for the expression x > 0 and x < 10 it will first process x > 0 and then x < 10.

However, if it happens that x = -1, the first expression x > 0 will be equal to False and then there is no point to evaluate the second expression. By definition, if one of the expression of an and is False, the whole expression is also False.

Python avoids processing extra expressions when the result is already known. This is know as short-circuiting the evaluation. Short-circuiting the evaluation lead to a useful technique known as the guard pattern. Let us see why it is needed with the following example.

x: int = 10
y: int = 5

x > 0 and x / y == 2

Everything works fine until now. But what does it happen if we change the value of y to 0?

x: int = 10
y: int = 0

x > 0 and x / y == 2

We get an error because you cannot have 0 as a denominator in a division. We can use the guard pattern to place a guard expression that let us check if y != 0. Let us see what happens now.

x: int = 10
y: int = 0

x > 0 and y != 0 and x / y == 2

No errors appear now because Python stops evaluating expressions when it notices that y != 0 == False. And this is the beauty of using the guard pattern!

---

1

This Jupyter Notebook is based on Chapter 3 and 5 of [Sev16]; and Chapter 5 and 7 of [Dow15].