Iteration 1 #

Introduction #

This chapter introduces the notion of a loop. In particular, we introduce the while statement together with the break and continue statements. Some remarks on the termination of the loops and additional examples are also presented.

The `while` Statement#

Computers are good in repeating boring tasks, they do this faster and more accurate than people. A block of code that is executed several times is called a loop. Each repetition of instructions within a loop is called an iteration. One fo the loop statements we can use in Python is called the while loop. A while loop is defined as follows.

while termination_condition:
    # body

You start with the while keyword, followed by a termination condition, followed by a colon. The next lines contain the body of the loop. The body of a loop is a sequence of Python statements (one or more statements) that are executed during every iteration of the loop.

The flow of execution for a while statement is as follows:

Determine whether the termination condition is True or False.
If False, exit the while statement and continue with the next statement outside of the loop.
If the condition is True, run the body and go back to step 1.

This type of flow is called a loop because the third step loops back to the top. Let us see an example.

# While statement
n: int = 0

while n < 5:
    n = n + 1  # Same as n += 1
    
print(n)

In the previous cell, we declare the variable n and we initialize it to zero. This happens outside of the loop. Then, we define a while loop. We use first the while keyword followed by the termination condition, followed by a colon. The termination condition of this loop (n < 5) states that the while loop will be executed while the value of n is strictly less than 5. The body of the loop (n = n + 1) is an assignment statement where we increment n by 1.

Let us add some print statements to see how the previous while loop is being executed.

# While statement
n: int = 0
iteration: int = 1
print('Initial value n =', n)

while n < 5:
    print('Iteration', iteration, ': n =', n)
    n += 1          # Same as n = n + 1
    iteration += 1  # Same as iteration = iteration + 1
    
print('Final value n =', n)

Initial value n = 0
Iteration 1 : n = 0
Iteration 2 : n = 1
Iteration 3 : n = 2
Iteration 4 : n = 3
Iteration 5 : n = 4
Final value n = 5

Loop Termination #

Suppose you want to countdown and print a value, we need to loop.

# Countdown program
n: int = 10
iteration: int = 1
print('Initial value n =', n)

while n > 0:
    print('Iteration', iteration, ': n =', n)
    n -= 1          # Same as n = n - 1
    iteration += 1  # Same as iteration = iteration + 1

print('Final value n =', n)

Initial value n = 10
Iteration 1 : n = 10
Iteration 2 : n = 9
Iteration 3 : n = 8
Iteration 4 : n = 7
Iteration 5 : n = 6
Iteration 6 : n = 5
Iteration 7 : n = 4
Iteration 8 : n = 3
Iteration 9 : n = 2
Iteration 10 : n = 1
Final value n = 0

The body of the loop should change the value of some variables that are used in the condition in order to ensure termination of the loop.

while True: print('Hello')

The while loop above will never terminate, this is a so-called infinite loop.

When writing programs it is important to convince yourself that the program terminates.

In the case of the countdown program, we can prove that the loop terminates: if n is zero (0) or negative, the loop exits. Otherwise, n gets smaller in each iteration of the loop, so eventually we have to get to zero (0).

Reasoning that loops terminate is not always trivial, consider for instance.

n: int = 5
iteration: int = 1
print('Initial value n =', n)

while n != 1:
    print('Iteration', iteration,': n =', n)
    
    if n % 2 == 0:  # n is even
        n = n / 2
    else:           # n is odd
        n = n * 3 + 1
        
    iteration += 1
        
print('Final value n =', n)

Initial value n = 5
Iteration 1 : n = 5
Iteration 2 : n = 16
Iteration 3 : n = 8.0
Iteration 4 : n = 4.0
Iteration 5 : n = 2.0
Final value n = 1.0

The condition for this loop is n != 1, so the loop will continue until n is 1, which makes the condition False. Since n sometimes increases and sometimes decreases, there is no obvious proof that n will ever reach 1, or that the program terminates.

For some particular values of n, we can prove termination. For example, if the starting value is a power of two, n will be even every time through the loop until it reaches 1.

The `break` Statement #

It is possible to enforce the termination of a loop via the break statement. Once your program flow reaches the break statement, all the code following the statement within the loop body won’t be executed!

The following shows the flowchart of the break statement.

Flowchart of the break statement.

Let us see an example.

while True:
    print('Print once!')
    break
    print("The rest won't be printed")

Print once!

The previous loop is executed just once due to the break statement. Once the break statement is executed, the program exits and the rest of the statements within the loop’s body are not executed.

Now, suppose you are processing the user’s input. The user eters any string and as soon as you get the string value done you need to terminate the program.

count_words: int = 0

while True:
    line: str = input('> ')
    if line == 'done':
        break
        
    count_words += 1  # Same as count_words += count_words + 1
    
print('The number of words is', count_words)

---------------------------------------------------------------------------
StdinNotImplementedError                  Traceback (most recent call last)
Cell In[6], line 4
count_words: int = 0
while True:
----> 4     line: str = input('> ')
   if line == 'done':
       break

File /opt/hostedtoolcache/Python/3.8.15/x64/lib/python3.8/site-packages/ipykernel/kernelbase.py:1172, in Kernel.raw_input(self, prompt)
"""Forward raw_input to frontends

Raises
------
StdinNotImplementedError if active frontend doesn't support stdin.
"""
if not self._allow_stdin:
-> 1172     raise StdinNotImplementedError(
       "raw_input was called, but this frontend does not support input requests."
   )
return self._input_request(
   str(prompt),
   self._parent_ident["shell"],
   self.get_parent("shell"),
   password=False,
)

StdinNotImplementedError: raw_input was called, but this frontend does not support input requests.

Do It Yourself!

Try to rewrite the while loop without the break statement.

# Remove this line and add your code here

The `continue` Statement #

Sometimes you want to finish the execution of the loop body for specific iterations. In that case, you want to stop the current iteration and continue with the next one. To do so, you can use the continue statement.

The following shows the flowchart of the continue statement.

Flowchart of the continue statement.

Let us see how to use the continue statement with the following example.

iteration: int = 0

while iteration <= 5:
    iteration += 1
    
    # Do not print anything in iteration 2
    if iteration == 2:
        continue
        print('Skip this text!')
        
    print(f'Iteration {iteration}')    

Iteration 1
Iteration 3
Iteration 4
Iteration 5
Iteration 6

In the previous example, we create the iteration variable and we set it to zero. Then, we introduce a while loop that loops while iteration is equal to or less than 5 (iteration <= 5). The first statement within the loop body increments the iteration value by 1. (So we guarantee that the program terminates at some point!) Then, if the value of the iteration variable is equal to 2, the iteration will be interrupted and the rest of the loop body won’t be executed. That is, neither the “Skip this text!” nor the “Iteration iteration” will be executed. Otherwise, the “Iteration iteration” message will be printed.

Let us check another example that combines both the break and continue statements.

while True:
    instruction = input('What to do next? ')
    
    if instruction == 'quit':
        break
    
    if instruction == 'skip':
        continue
        print('Skip this line')
        
    print('Your instruction is ' + instruction)

In this program we ask for input to the user and we print a message saying “Your instruction is instruction”. However, if the input is equal to “quit”, the program will end. Otherwise, if the input is equal to “skip”, the current iteration will stop just before printing the message and will continue with the next iteration.

Do It Yourself!

Try to rewrite the while loop without the break and continue statements.

# Remove this line and add your code here

`while` Loops in Detail #

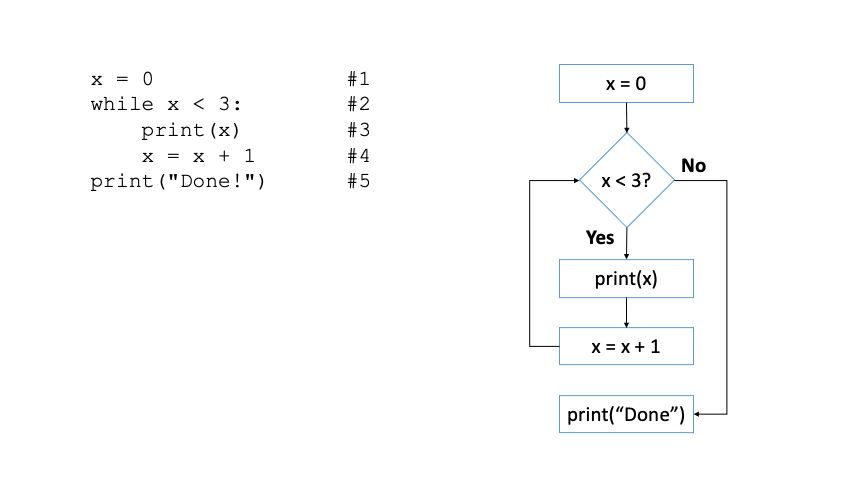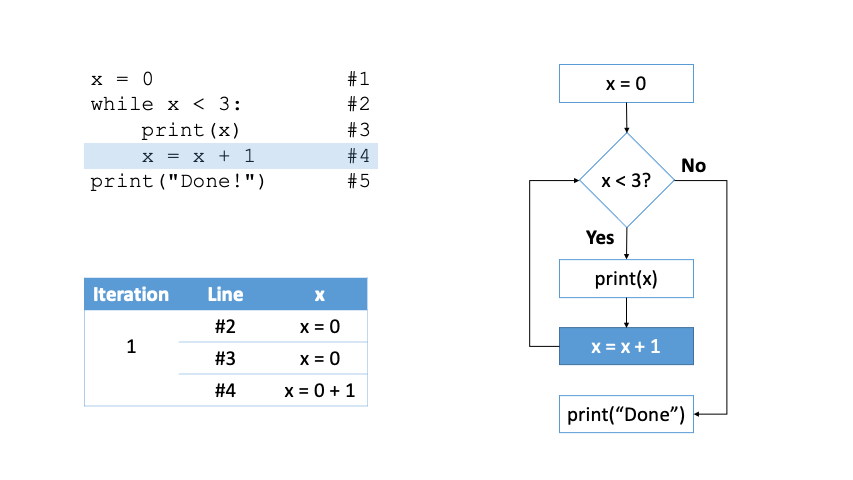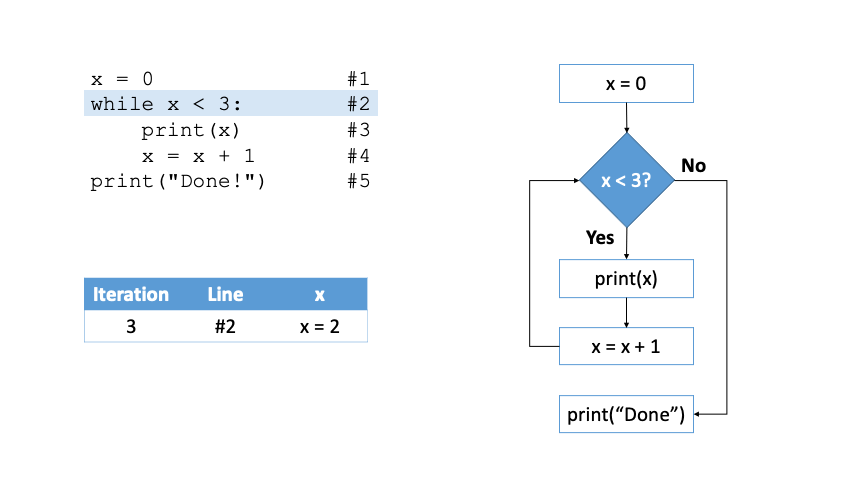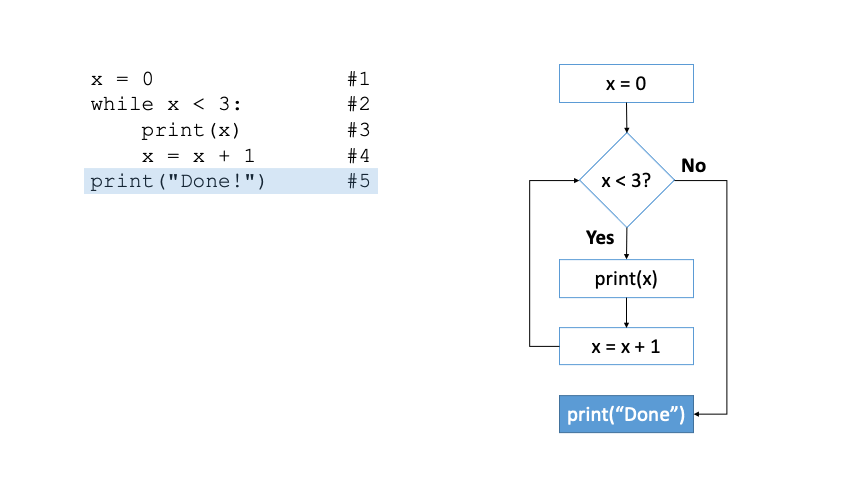
Let us consider the following cell to understand the flow of control of a while loop.

A while loop should always have a Boolean expression (termination condition). In the cell x < 10 (see line #2).
A while loop should have at least one statement in the body (see lines #3 and #4). Beware only the indented statements are part of the body, line #5 is not part of the body.
As long as the evaluation of the condition yields the Boolean value True (see line #2), the statements in the body are executed (see lines #3 and #4). After the execution of the body, the condition is re-evaluated.
If the evaluation of the condition yields the value False, the statement after the body is executed (see line #5).
Removing the indentation on line #4 leads to a non-terminating loop. Why?

x: int = 0          #1
while x < 10:       #2
    print(x)        #3
    x = x + 1       #4
print('Done!')      #5

The program above can be visualised as follows.

Flowchart of the first while-loop program.

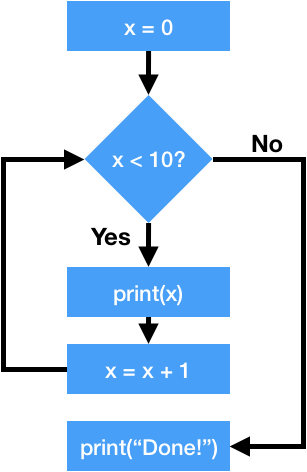
Let us see another example.

Animmated while-loop program.

x: int = 0          #1
while x < 10:       #2
    print(x)        #3
x = x + 1           #4
print('Done!')      #5

The program above can be described as follows.

In line #1, we initialize variable x to 0.
In line #2, we write down the termination condition of the while loop (x < 10).
Line #3 contains the body of the loop; there is only one statement in charge of printing the content of x.
As you can notice the value of x is not modified within the while body, meaning that x won’t ever reach 10, and the loop will never terminate.
In line #4, we increment the value of x by 1, and in line #5 we print the text “Done!”.
Given that the loop never terminates, line #4 and #5 won’t ever be reached.

Flowchart of the second while-loop program.

The execution of the loop can always be terminated via a break statement. See line #6 in the cell below.
Often the break statement is used in combination with a conditional. See lines #5 and #6.
This conditional should be part of the loop body, so intended.

Let us see yet another example!

x: int = 0          #1
while True:         #2
    print(x)        #3
    x = x + 1       #4
    if x >= 10:     #5
        break       #6
print('Done!')      #5

The program above can be described as follows.

In line #1, we initialize variable x to 0.
In line #2, we write True as the termination condition of the while loop. This means that if at some point you want to terminate the loop, you must have a break statement.
Line #3 starts with the body of the loop. In this line we print the content of x (print(x)).
Line #4 is still part of the loop body
As you can notice the value of x is not modified within the while body, meaning that x won’t ever reach 10, and the loop will never terminate.
In line #4, we increment the value of x by 1.
In line #5, we introduce a conditional statement (x >= 10) that if True, will break the loop (see line #6). We know that we will reach a termination state because x is being incremented by 1 in every iteration, and we can expect it to reach 10 at some point.
Once the execution of the loop is done, we print the text “Done!” in line #7.

Flowchart of the third while-loop program.

Loop Examples #

Square Roots#

Loops are often used in programs that compute numerical results by starting with an approximate answer and iteratively improving it.

For example, one way of computing square roots of a number is Newton’s method. Suppose that you want to know the square root of a number \(a\). If you start with almost any estimate, \(x\), you can compute a better estimate with the following formula:

\(y = \frac{x + \frac{a}{x}}{2}\)

For example, if \(a\) is 4 and \(x\) is 3, we get:

a: int = 4
x: int = 3
y: int = (x + a / x) / 2
y

The result is closer to the correct answer (\(\sqrt{4} = 2\)). If we repeat the process with the new estimate, it gets even closer.

x = y
y = (x + a / x) / 2
y

After a few more iterations the result gets more precise.

x = y
y = (x + a / x) / 2
y

x = y
y = (x + a / x) / 2
y

After a couple more iterations the value of \(y\) is equal to \(x\) and thus we can stop.

x: int = 1
a: int = 4

while True:
    print(x)
    y: int = (x + a / x) / 2
    
    if y == x:
        break
    
    x = y

For most values of a this works fine, but in general it is dangerous to test equality on floating-point numbers. Floating-point values are only approximately right: most rational numbers, like 1/3, and irrational numbers, like \(\sqrt{2}\) cannot be represented exactly with a float.

Rather than checking whether x and y are exactly equal, it is safer to use the built-in function abs to compute the absolute value, or magnitude, of the difference between them.

x: int = 3
a: int = 4
epsilon: float = 0.00000000000001

while True:
    print(x)
    y: int = (x + a / x) / 2
    
    if abs(y - x) < epsilon:
        break
        
    x = y

Where epsilon has a value like 0.00000000000001 that determines how close is close enough.

Adding Numbers#

Suppose we want to add all numbers to a number provided via input.

number_str: str = input()
number = int(number_str)
total: int = 0

while number > 0:
    total += number  # Same as total = total + x
    print('total =', total)
    number -= 1      # Same as number = number - 1
    print('number =', number)

print('total =', total)### Modified Addition

In the following program, we want to:

1. Ask the user for an integer number.
1. Initialize a counter to `0`.
1. Initialize a `total` variable to `0`
1. If the counter is **even**, we add it to the `total`.
1. If not, we do nothing.
1. We increment the counter by `1`, and we go back to step 4.
1. We loop until the counter is greater than the input integer number.

Modified Addition#

In the following program, we want to:

Ask the user for an integer number.
Initialize a counter to 0.
Initialize a total variable to 0
If the counter is even, we add it to the total.
If not, we do nothing.
We increment the counter by 1, and we go back to step 4.
We loop until the counter is greater than the input integer number.

input_: str = input('Give a number > 0:')
number: int = int(input_)
counter: int = 0
total: int = 0

while counter <= number:
    print('counter =', counter)
    
    if counter % 2 == 0:
        total += counter
        print('total =', total)
        
    counter += 1
    
print('total =', total)

1: This Jupyter Notebook is based on Chapter 3 and 5 of [Sev16]; and Chapter 5 and 7 of [Dow15].

Learning Python by doing

Iteration

Contents

Iteration 1 #

Introduction #

The `while` Statement#

Loop Termination #

The `break` Statement #

The `continue` Statement #

`while` Loops in Detail #

Loop Examples #

Square Roots#

Adding Numbers#

Modified Addition#

Learning Python by doing

Iteration

Contents

Iteration 1#

Introduction #

The while Statement#

Loop Termination #

The break Statement #

The continue Statement #

while Loops in Detail #

Loop Examples #

Square Roots#

Adding Numbers#

Modified Addition#

Iteration 1 #

The `while` Statement#

The `break` Statement #

The `continue` Statement #

`while` Loops in Detail #