Recursion
Contents
Recursion 1#
Recursion#
One of the most powerful but also intriguing features of a programming is recursion.
An extremely simple definition of recursion is defining a computation in terms of itself.

If translated to our Python world, one could say that you define a function in terms of itself. That is, in the definition of the function body a function call to the function you are defining is used.
Let us make this more concrete by means of a simple example.
def countdown(n : int) -> None:
""" Prints by means of recursion decreasing values from n to 1
and prints "Ready!" for n = 0.
"""
if n <= 0:
print('Ready!')
else:
print(n)
countdown(n - 1)
If n is 0 or negative, it outputs the word, “Ready!”.
Otherwise, it outputs n and then calls a function named countdown passing n - 1 as an argument.
countdown(3)
3
2
1
Ready!
The execution of countdown begins with n=3, and since n is greater than 0,
it outputs the value 3, and then calls itself…
The execution of countdown begins with n=2, and since n is greater than 0,
it outputs the value 2, and then calls itself…
The execution of countdown begins with n=1, and since n is greater than 0,
it outputs the value 1, and then calls itself…
The execution of countdown begins with n=0, and since n is
not greater than 0, it outputs the word, “Ready!” and then returns.
The countdown that got n=1 returns.
The countdown that got n=2 returns.
The countdown that got n=3 returns.
And then you are back in __main__.
A function that calls itself is recursive; the process of executing it is called recursion.
We can write a function that prints a string n times.
def print_n(s : str, n : int) -> None:
""" Prints the string represented by the parameter "s" and recursively
calls itself with a string "s+ +s" as long as "n > 0".
"""
if n <= 0:
return
print(s)
print_n(f'{s} {s}', n - 1)
print_n("Machine Learning", 5)
Machine Learning
Machine Learning Machine Learning
Machine Learning Machine Learning Machine Learning Machine Learning
Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning
Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning Machine Learning
If n <= 0 the return statement exits the function.
The flow of execution immediately returns to the caller, and the remaining lines of the function are not executed.
The rest of the function is similar to countdown: it displays the string represented by the variable s and then calls itself to display
s n − 1 times.
For simple examples like this, it is probably easier to use a for loop.
But we will come across examples that are much harder to write with a for loop than with recursion, for instance calculating the factorials or the fibonacci numbers, see later.
However, some care is needed! It is very easy to create a recursive function that does not terminate, it is as easy as creating a loop that does not terminate, when does a loop not terminate?
Do It Yourself!
Create the recursive version of the function sum_digits. As before, the function takes a number as input and returns the sum of all the digits of such number. For instance, the output for the input 13450 is 13.
# Remove this line and add your code here
Infinite Recursion#
Recursion is very powerful and convenient, but there is also a risk, we have to ensure that the recursion terminates.
So, as a programmer you have to take care of formulating a correct base case that terminates the recursion.
If you consider both the countdown and the print_n function you will see that the base case is formulated as
n <= 0, the reason for using n <= 0 is to ensure termination of the recursion even if these functions are called with a negative number.
If you encounter an infinite recursion by accident, review your function to confirm that there is a base case that does not make a recursive call.
And if there is a base case, check whether you are guaranteed to reach it.
The print_n recursive function, terminate elegantly for values of n < 10.
print_n('Machine Learning', -10)
def print_n(s : str, n : int) -> None:
""" Prints the string represented by the parameter "s" and recursively
calls itself with a string "s+ +s" as long as "n != 0".
"""
if n == 0:
return
print(s)
print_n(s + " " + s, n - 1)
print_n("Machine Learning", -2)
Do It Yourself!
Which is the base case of the recursive function sum_digits?
More Recursion#
A recursive definition is similar to a circular definition, in the sense that the definition contains a reference to the thing being defined.
In normal life, this does not make much sense, but when programming it is extremely handy.
Consider the recursive definition of the factorial function:
\(0! = 1 \\ n! = n * (n-1)!\)
This definition says that the factorial of \(0\) is \(1\), and the factorial of any other value, \(n\), is \(n\) multiplied by the factorial of \(n − 1\).
So 3! is 3 times 2!, which is 2 times 1!, which is 1 times 0!.
Putting it all together, 3! equals 3 times 2 times 1 times 1, which is 6.
If you can write a recursive definition of something, you can write a Python program to evaluate it.
The first step is to decide what the parameters should be. In this case it should be clear that factorial takes an integer:
def factorial(n : int) -> int:
"""Calculates the factorial of its argument n."""
if n == 0:
return 1
If the argument is \(0\) than we return \(1\), otherwise we have to make a recursive call to factorial to calculate
the value of \(n-1\) and multiply this by \(n\).
def factorial(n : int) -> int:
"""Calculates the factorial of its argument n."""
if n == 0:
return 1
else:
i_fac_value : int = factorial(n - 1)
result = n * i_fac_value
return result
factorial(100)
The body of the else part can be written more compactly.
def factorial(n : int) -> int:
"""Calculates the factorial of its argument n."""
if n == 0:
return 1
else:
return n * factorial(n - 1)
factorial(100)
If the last statement of the function contains the a call to the recursive function, we call this tail recursion, we can replace the recursive function by a loop.
def factorial(n : int) -> int:
"""Calculates the factorial of its argument n."""
rf : int = 1
while n > 0:
rf *= n
n -= 1
return rf
factorial(100)
The factorial function, but now with proper tests.
def factorial(n : int) -> int:
"""Calculates the factorial of its argument n.
>>> factorial(0) # base case
1
>>> factorial(10) # arbitrary number
3628800
"""
if n == 0:
return 1
else:
i_fac_value : int = factorial(n - 1)
result : int = n * i_fac_value
return result
factorial(10)
import doctest
doctest.testmod(verbose=True) # with details
Do It Yourself!
Add at least two tests to check the output of the sum_digits function. Check the base case output and other arbitrary case. Verify the output given by the doctest module.
# Remove this line and add your code here
More Recursion Examples#
Yet another famous recursive mathematical function is the fibonacci function.
Growth of trees, biological ones, follow this principle.
fibonacci(0) = 0
fibonacci(1) = 1
fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)
def fibonacci(n : int) -> int:
"""Calculates the fibonacci number of its argument.
>>> fibonacci(0) # base case 0
0
>>> fibonacci(1) # base case 1
1
>>> fibonacci(13) # arbtriry number
233
"""
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
fibonacci(15)
doctest.testmod(verbose=True) # with details
[fibonacci(n) for n in range(20)]
fibonacci(35)
Why is it so slow?
Let us count the number of fib calls.
def fib_calls(n: int) -> int:
""" Counts the number of calls to fib to compute fib(n).
"""
if n <= 1:
return 0
else:
return 2 + fib_calls(n - 2) + fib_calls(n - 1)
fib_calls(35)
Many Fibonacci values get recomputed over and over again.
Keep in mind that there are only 35 Fibonacci values smaller than fib(35).
Do It Yourself!
Create the recursive function countup, which takes an integer as parameter and prints numbers from 1 until the input number in a recursive way.
# Remove this line and add your code here
Towers of Hanoi#
Tower of Hanoi is a mathematical puzzle where we have three rods and n disks. The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
Only one disk can be moved at a time.
Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack i.e. a disk can only be moved if it is the uppermost disk on a stack.
No disk may be placed on top of a smaller disk.
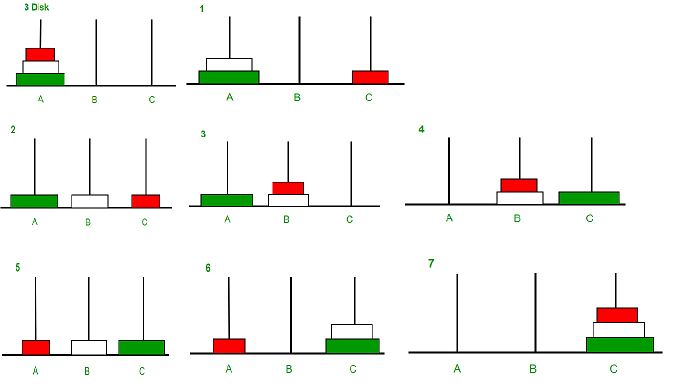
def towers_of_hanoi(n : int , source : str, destination : str, auxiliary : str) -> None:
# print("n = ", n, "src = ", source, "dst = ", destination, "aux = ", auxiliary)
if n == 1:
print("Move disk 1 from source", source, "to destination", destination)
return
towers_of_hanoi(n - 1, source, auxiliary, destination)
print("Move disk", n, "from source", source, "to destination", destination)
towers_of_hanoi(n - 1, auxiliary, destination, source)
# Driver code
n = 2
towers_of_hanoi(n, 'A', 'B', 'C')
Memos#
Inefficiency in recursive definitions#
The recursion depth is the number of concurrently active invocations.
Recursive definitions can be very inefficient, even if the recursion depth is moderate.
Exponential blowup when each call can give rise to multiple recursive calls.
How to do better?
Improving efficiency in recursive definitions#
Various techniques available:
Cache (memorize) previously computed results, and reuse them without recalculation.
Introduce extra parameters and/or extra results, to improve efficiency.
When performing calculations, specially in case of calculation that involve recursion, it may be advisable to store intermediate results.
Consider the fibonacci function, when you are calculating the fibonacci number for larger values, you will observe that this will take some time.
The larger the value, the more time it will take.
The observation is that when calculating fibonacci numbers you will calculate the value for smaller values multiple times.
The calculation of fibonacci numbers can be more efficient by memoizing intermediate values.
known_fibs = {0:0, 1:1}
def fibonacci(n : int) -> int:
"""Calculates the fibonacci number of its argument by means of a cache.
>>> fibonacci(0) # base case 0
0
>>> fibonacci(1) # base case 1
1
>>> fibonacci(13) # arbitrary number
233
"""
if n in known_fibs:
return known_fibs[n]
res = fibonacci(n - 1) + fibonacci(n - 2)
known_fibs[n] = res
return res
fibonacci(350)
#print(known_fibs)
doctest.testmod(verbose=True) # with details
known_fibs is a dictionary that keeps track of the Fibonacci numbers we already know. It starts with two items: 0 maps to 0 and 1 maps to 1.
Whenever fibonacci is called, it checks known cases.
If the result is already there, it can return immediately.
Otherwise it has to compute the new value, add it to the dictionary, and return it.

